Par Nicolas Gambardella
Les dernières statistiques d’Israël et du Royaume-Uni sur la covid-19 dans les populations vaccinées et non vaccinées sont devenues virales. L’une des principales raisons de ce succès dans certains milieux est qu’elles montrent apparemment que les vaccins contre le virus de la covid ne sont plus efficaces ! Ce n’est bien entendu pas le cas. Si les anticorps circulants produits par une vaccination complète semblent diminuer avec une demi-vie d’environ six mois, la protection reste très forte contre la maladie, qu’elle soit modérée ou sévère. La protection contre l’infection reste également robuste pendant les premiers mois suivant la vaccination, quel que soit le variant. Comment expliquer dès lors le résultat apparemment paradoxal selon lequel le taux de mortalité par covid est le même dans les populations vaccinées et non vaccinées ? Plusieurs facteurs peuvent être mis en cause. Par exemple, dans la plupart des ensembles de données utilisés pour calculer l’efficacité, les personnes pré-infectées non vaccinées ne sont pas retirées. Cependant, je voudrais aujourd’hui mettre en avant une autre raison car je pense qu’il s’agit d’un piège dans lequel les apprentis analystes de données tombent très fréquemment : Le paradoxe de Simpson.
Le paradoxe de Simpson se produit quand une tendance présente dans plusieurs sous-populations disparaît, voire s’inverse, lorsque toutes ces populations sont aggrégées. Cela est souvent dû à des facteurs de confusion cachés. La situation est bien illustrée dans la figure suivante obtenue de Wikimedia commons. Alors que la corrélation entre Y et X est positive dans chacune des cinq sous-populations, cette corrélation devient négative si l’on ne distingue pas les sous-populations.
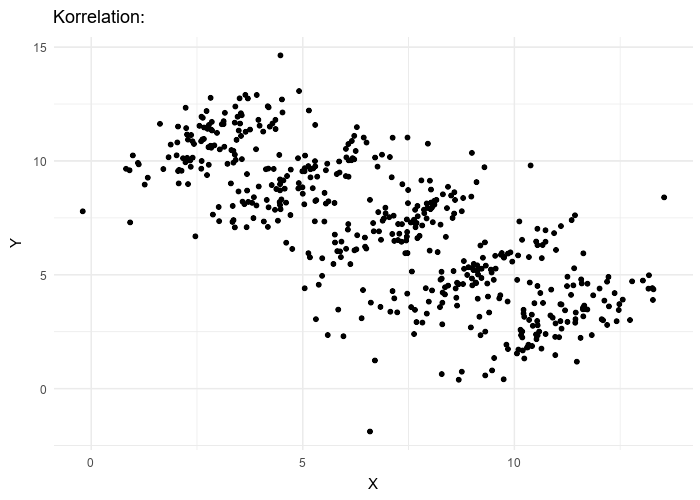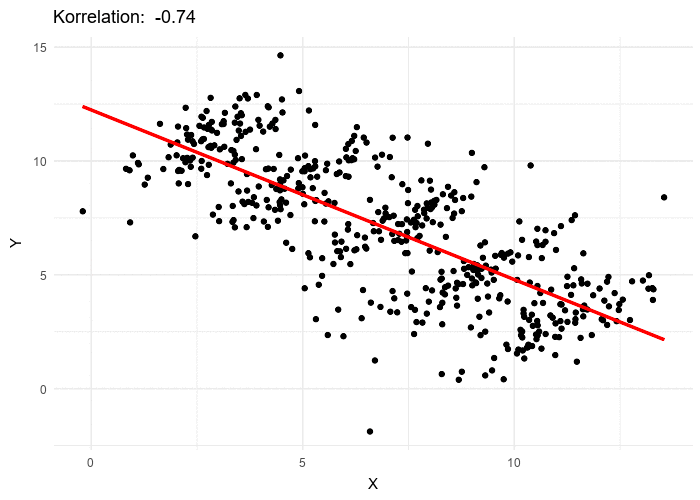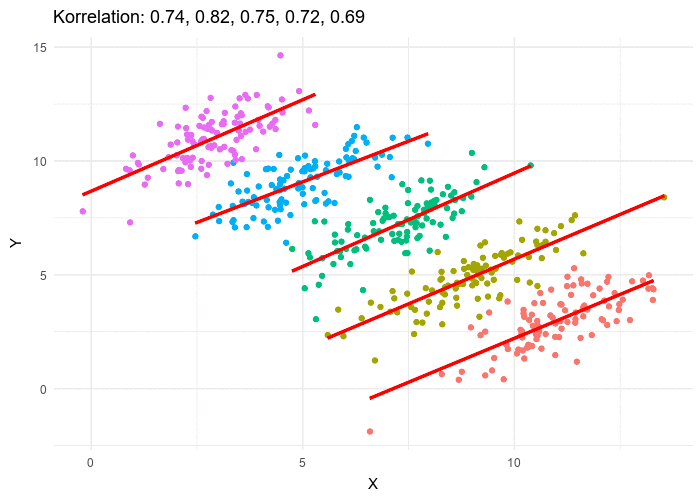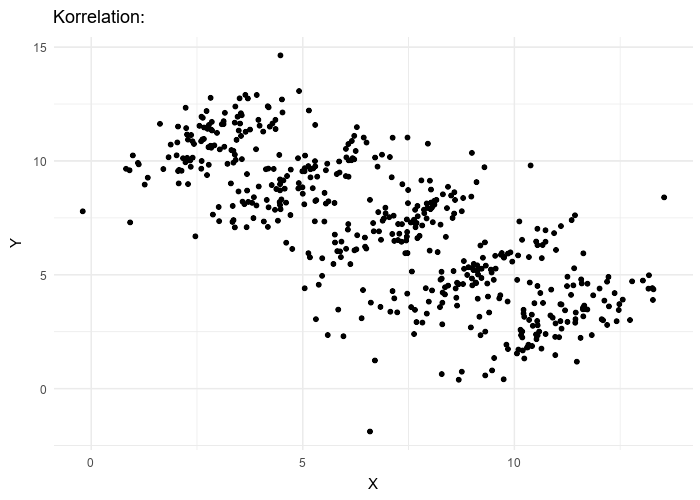
Qu’en est-il de la vaccination contre le SRAS-CoV-2 ? Jeffrey Morris explique sur son blog l’impact du paradoxe de Simpson sur l’analyse des données d’Israël de manière précise et éclairante, bien mieux que je ne pourrais le faire. Cependant, son excellente explication est assez longue et détaillée, et en anglais. J’ai donc pensé que je pourrais en donner une version courte ici, avec une population imaginaire, simplifiée, bien que réaliste.
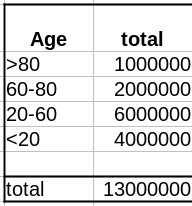
Comme évoqué dans un précédent billet, la donnée cruciale ici est la structure de la population par classe d’âge . Pour simplifier, nous prendrons une pyramide des âges assez simple, proche de ce que l’on observe dans les pays développés, c’est-à-dire homogène avec seulement une diminution au sommet, ici 1 million de personnes par décennie, et 1 million pour toutes les personnes de plus de 80 ans.
La première variable importante est le taux de vaccination. Comme les campagnes de vaccination ont commencé avec les populations âgées et que l’hésitation vaccinale diminue fortement avec l’âge, le taux de vaccination est beaucoup plus faible dans les populations plus jeunes.
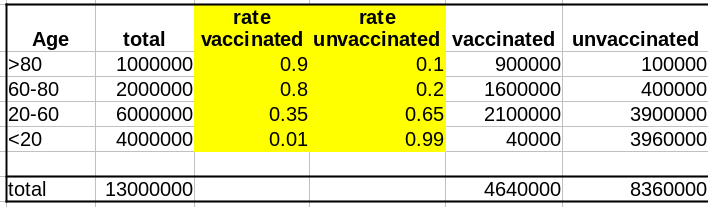
La deuxième variable importante est le taux de létalité de la maladie (Infection Fatality Rate, IFR) pour chaque tranche d’âge. Là aussi, l’IFR est beaucoup plus faible dans les populations les les plus jeunes. Et c’est là que se trouve le nœud du problème : taux de vaccination et taux de létalité ne sont pas des variables indépendantes ; les deux sont liées à l’âge.
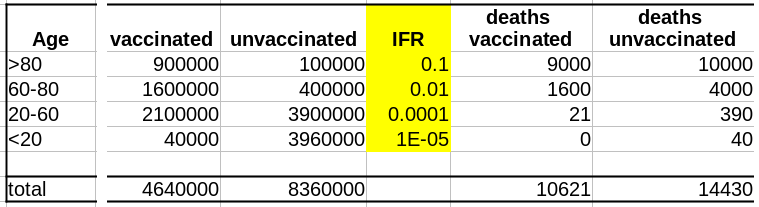
Supposons que notre vaccin ait une efficacité absolue de 90 % et que, pour simplifier, cette efficacité ne dépende pas de l’âge. Le nombre de décès dans la population non vaccinée est :
Deaths unvaccinated = round(unvaccinated * IFR)
La fonction arrondi est pour éviter les fractions de personnes mortes. Le nombre de décès dans la population vaccinée est de :
Deaths vaccinated = round(vaccinated * IFR * 0.1)
où 0.1 = (100 – efficacy)/100
Maintenant que nous avons le nombre de décès dans chacune de nos populations, vaccinées ou non, nous pouvons calculer les taux de mortalité, c’est-à-dire décès/population, et calculer l’efficacité comme suit :
(death rate unvaccinated – death rate vaccinated)/(death rate unvaccinated)*100
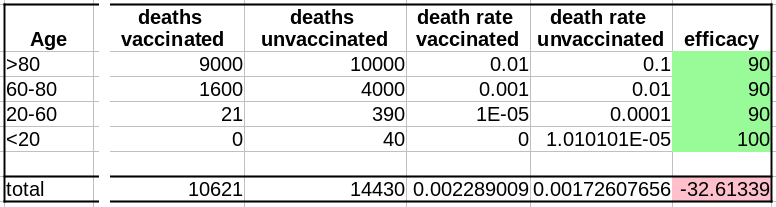
Sans surprise, l’efficacité pour toutes les tranches d’âge est de 90%. Les 100% pour les <20 ans viennent du fait que 0,04 décès est arrondi à 0.
Cependant, si l’on fusionne toutes les tranches d’âge, l’efficacité disparaît complètement ! De plus, il semblerait que le vaccin augmente le taux de mortalité ! Le fait de ne pas être vacciné présente une protection contre le décès de 32% !
Il s’agit bien sûr d’un résultat erroné (nous le savons ; nous avons créé l’ensemble de données avec une efficacité vaccinale réelle de 90% !). Cet exemple utilise l’efficacité d’un vaccin. Cependant, le paradoxe de Simpson guette souvent l’apprenti analyste de données au tournant. Les facteurs de confusion doivent être recherchés avant toute analyse statistique, et les populations doivent être stratifiées en conséquence.