Month: April 2020

Par Nicolas Gambardella

[Version anglaise]

Les tests sont au cœur de la plupart, sinon de la totalité, des stratégies proposées pour lutter contre la pandémie de Covid-19. La famille d’approches « identifier et éliminer » repose sur l’identification des cas de personnes infectées par le virus du SRAS-CoV-2 et sur leur isolement ou leur traitement. La famille d’approches « acquérir une immunité » repose sur l’identification des personnes qui ont été infectées par le passé et qui sont maintenant immunisées contre la maladie, afin de pouvoir les libérer. Enfin, les stratégies de dépistage influent également sur l’estimation de la létalité de cette maladie (voir remarque à la fin de ce billet).

Au moment où j’écris ces lignes (13 avril 2020), le gouvernement britannique vient de rejeter tous les tests d’anticorps sanguins qu’il a testés, c’est-à-dire les tests qui identifient les personnes ayant été en contact avec le virus dans le passé, et supposées être immunisées. Au même moment, on peut lire de nombreux rapports de « tests peu fiables », ne détectant « qu’un tiers des cas ». Comment se fait-il que des professionnels aient conçu des tests si « mauvais » ? Quelle doit être la qualité d’un test pour qu’il soit utile ? Et pourquoi un test qui repère correctement 90 % des personnes infectées ne vaut-il pas mieux qu’un pile ou face pour dire si vous êtes réellement infecté ou non ?

Allons droit au but afin que vous puissiez arrêter de lire et reprendre des activités de confinement plus agréables, si vous le souhaitez. Puis nous introduirons les maths.

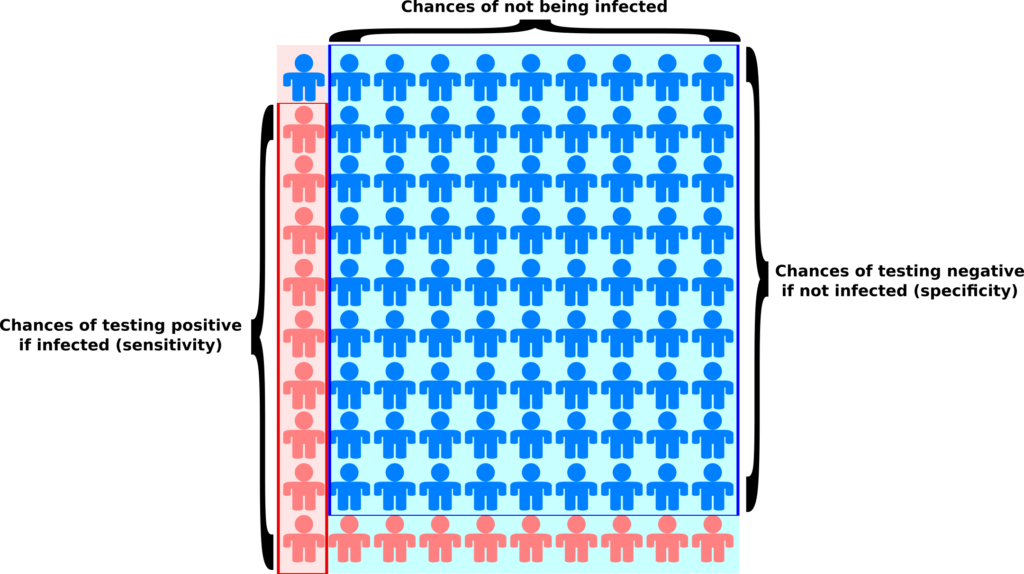
Si nous disposons d’un test qui identifie correctement 90 % des personnes infectées (une sensibilité de 90 %), et qui signale correctement comme négatif 90 % des personnes non infectées (une spécificité de 90 %), mais qu’en même temps 90 % de l’ensemble de la population n’a jamais été infectée (une prévalence de 10 %), et que nous testons ensuite un échantillon aléatoire de cette population, nous obtiendrons la même quantité de vrais et faux positifs. En d’autres termes, si vous êtes testé positif, les chances que vous soyez réellement immunisé sont… 50 % ! Vous pouvez facilement comprendre ça avec l’image suivante.

Le fond bleu pâle représente la population qui n’a pas été infectée, tandis que le fond rose pâle représente la population qui a été infectée (la prévalence). Le test des personnes roses est positif, tandis que celui des personnes bleues est négatif. Comme vous pouvez le voir, il y a le même nombre de personnes roses (9) sur les fonds rose pâle et bleu pâle. Oui, le test est positif pour 9 personnes infectées sur 10, alors qu’il n’est positif que pour 1 personne non infectée sur 10. Mais il y a 9 personnes non infectées pour chaque personne infectée, ce qui fait pencher la balance dans l’autre sens.

Ce n’était qu’un exemple, simplifié puisque j’ai supposé des sensibilité et spécificité égales. Pour un test détectant la présence de quelque chose, la sensibilité serait généralement inférieure à la spécificité (manquer quelque chose sera plus probable que signaler quelque chose qui n’est pas là). Par ailleurs, comment les chiffres changent-ils lorsque nous modifions la prévalence, c’est-à-dire la proportion de la population qui a été infectée ? Venons-en aux maths.

Le calcul est basé sur le théorème de Bayes, du nom du révérend Thomas Bayes. Ce billet ne porte pas sur le théorème lui-même, sa signification ou sa démonstration. Si vous souhaitez en savoir plus, la chaîne YouTube 3Blue1Brown propose d’excellentes vidéos sur le sujet (en anglais) :

The quick proof of Bayes’ theorem

Bayes theorem

Pour aujourd’hui, acceptez juste l’affirmation suivante :

Vos chances d’être vraiment infecté si votre test est positif sont égales aux chances d’être infecté multipliées par les chances d’obtenir un test positif si vous être infecté, proportionnellement à la population dont le test est revenu positif (que les personnes aient été infectées ou non).

En mathématiques, on écrirait (P(X) étant la « probabilité de X » et la barre verticale « | » représentant une probabilité conditionnelle, à savoir la probabilité que le terme de gauche soit vrai si le terme de droite l’est) :

P(Infecté | Positif) = P(Infecté) x P(Positif | Infecté) / P(Positif)

Cette équation, le théorème de Bayes, vient du fait que :
P(Positif) x P(Infecté | Positif) = P(Infecté) x P(Positif | Infecté)
C’est évident si l’on considère l’image ci-dessous. Qu’on dessine le cercle de gauche d’abord, puis celui de droite ou le contraire, on obtient la même intersection.

Le dénominateur, P(Positif), représentant toutes les personnes testées positives, est la somme des personnes ayant correctement été testées positives après infection et de celles ayant incorrectement été testées positives alors qu’elles n’étaient pas infectées :

P(Positif) = P(Infecté) x P(Positif | Infecté) + P(NonInfecté) x P(Positif | NonInfecté)

Cette probabilité, P(Infecté | Positif), est particulièrement importante dans le cas des tests d’anticorps. Personne ne veut dire à une personne qu’elle est immunisée si elle ne l’est pas !

De la même façon, nous pouvons calculer les chances que quelqu’un ayant un test négatif ne soit effectivement pas infecté. Ceci est très important au début de l’épidémie, lorsque l’on veut éviter la propagation de la maladie par les gens infectés.

P(NonInfecté | Négatif) = P(NonInfecté) x P(Négatif | NonInfecté) / P(Négatif)

Le dénominateur, P(Négatif), représentant toutes les personnes testées négatives, est la somme des personnes ayant correctement été testées négatives en n’étant pas infectées et de celles ayant incorrectement été testées négatives bien qu’étant infectées :

P(Négatif) = P(NonInfecté) x P(Négatif | NonInfecté) + P(Infecté) x P(Négatif | Infecté)

Voyons ce que l’on obtient avec des valeurs numériques. Nous avons trois paramètres et leurs compléments. Disons que nous avons une maladie affectant 5 % de la population (la prévalence).
P(Infecté) = 0,05
P(NonInfecté) = 0,95

80 % des personnes infectées sont reconnues par le test (la sensibilité).
P(Positif | Infecté) = 0,8
P(Négatif | Infecté) = 0,2

95 % des personnes qui ne sont pas infectées ne présentent pas de test positif (la spécificité).
P(Négative | NonInfecté) = 0,95
P(Positif | NonInfecté) = 0,05

Alors, si vous êtes testé positif, quelles sont les chances que vous soyez vraiment immunisé ?

0,05 x 0,8 / (0,05 x 0,8 + 0,95 x 0,05) = 0,457

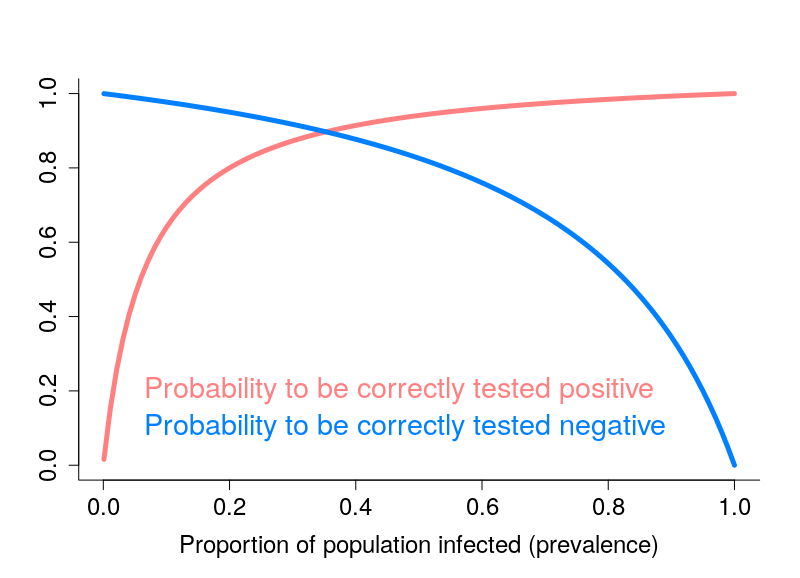
46 % ! En d’autres termes, il y 54 % de chances que vous ne soyez pas immunisé, bien que votre test soit positif… De la même manière, si votre test est négatif, les chances que vous soyez infectés sont de 0,2 %. Cela paraît négligeable, mais cela peut être suffisant pour laisser sortir un patient infectieux. De plus, ce chiffre augmente avec la prévalence. De combien ? Le graphique ci-dessous décrit l’évolution des probabilités d’être correctement testé positif ou négatif alors que la proportion de la population infectée augmente.

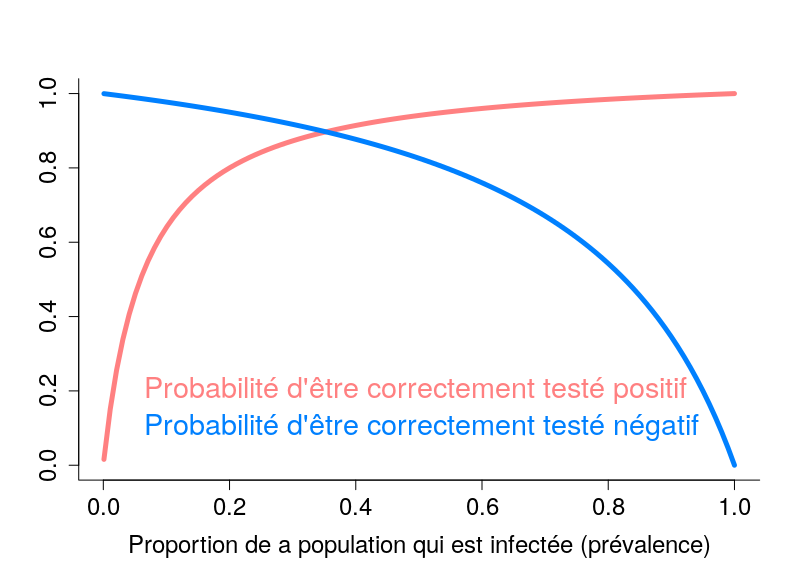
C’est plutôt déprimant. Une façon d’améliorer les résultats est évidemment de disposer de meilleurs tests. Cependant, le « retour sur investissement » s’amenuise à mesure que la qualité des tests s’améliore. Une autre solution, consiste à multiplier les tests, si possible avec des tests différents. C’est, par exemple, la base du test combiné pour la trisomie 21. Je vous laisse calculer les probabilités dans le cas de deux tests fournissant des résultats identiques.

Une remarque sur la létalité de Covid-19

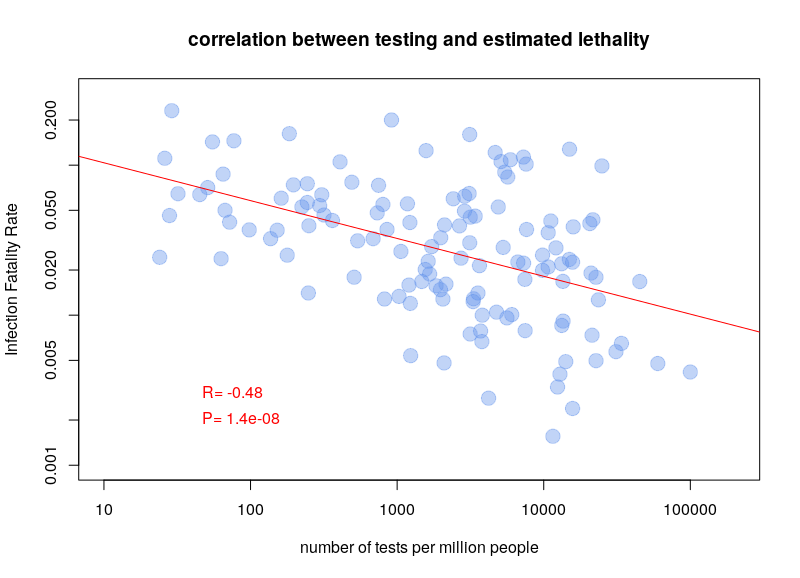
Pourquoi ai-je écrit plus haut que la précision des tests était pertinente pour estimer la létalité de la maladie ? Vous trouverez ci-dessous un graphique du rapport entre le nombre de décès par nombre de cas et le nombre de tests par million de personnes, pour tous les pays ayant déclaré au moins un décès et au moins dix tests (données du 10 avril 2020).

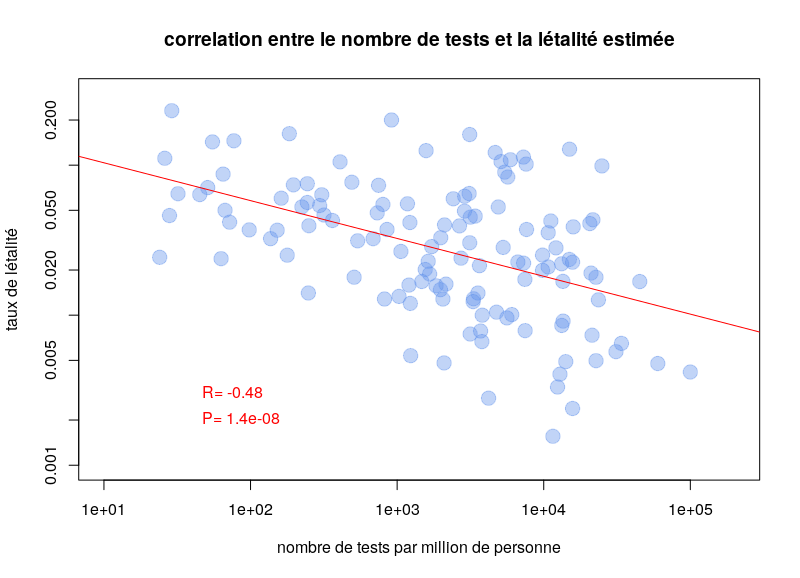
Il est assez clair qu’il existe une corrélation. Plus les tests sont nombreux, plus le nombre de décès estimé est faible. Cela montre que nous surestimons probablement la létalité de la maladie, et que nous sous-estimons sa prévalence (et donc son infectiosité). Que ce résultat soit exact ou non, la capacité à déduire correctement le nombre réel de personnes infectées ou immunisées est assez cruciale. En outre, la sensibilité et la spécificité des tests utilisés par les différents pays doivent être prises en compte lors de l’estimation de la prévalence et du taux de létalité.

By Nicolas Gambardella

[French version]

Testing is at the core of most, if not all, strategies proposed to fight the Covid-19 pandemic. The “identify and squash” family of approaches relies on identifying cases of people infected by the SARS-CoV-2 virus and isolate and/or treat them. The “get immune” family of approaches relies on identifying people who were infected in the past, and are now immune to the disease, so we can release them. Finally, testing strategies also affect the estimation of how lethal this disease is (see note at the end).

As I write this post (13 April 2020), the UK government just rejected all the blood antibody tests it assessed, the tests that identify people who were in contact with the virus in the past, and supposedly immune. In a similar vein, we can see many reports of “unreliable tests”, catching “only one-third of the cases”. How come professionals designed such “bad” tests? How good a test must be to be useful? And why is a test that correctly spots 90% of infected people not better than the flip of a coin at telling if you are actually infected or not?

There is a short and a long answer. I will give the short one first, so you can stop reading and go back to more enjoyable confinement activities if you so wish.

If we have a test that correctly identifies 90% of the people who were infected (a sensitivity of 90%), and correctly reports as negative 90% of people who were not infected (a specificity of 90%), but at the same time 90% of the whole population was never infected (a prevalence of 10%), and then we test a random sample of this population, we will get the same amount of true and false positive. In other words, if you are tested positive, the chances that you are actually immune is… 50%! You can easily grasp that on the picture below.

The light blue background represents the population that has not been infected while the light pink background represents the population that has been infected (the prevalence). The blue people are tested negative, while the pink people are tested positive. As you can see, we get the same amount of pink people (9) on light pink and light blue backgrounds. Yes, the test comes back positive 9 out of 10 infected people, while it comes back positive only 1 out of 10 non-infected people. But there are 9 non-infected people for each infected one, which tips the balance the other way.

Now, that was just one example, simplified since I assumed equal sensitivity and specificity. For a test detecting the presence of something, sensitivity would typically be lower than specificity (missing something will be more probable than reporting something that is not there). Also, how do the figures change when we change the prevalence, that is the proportion of the population that got infected? Let’s get to the actual calculations.

The basis for such calculus is the Bayes’ theorem, named after the Reverend Thomas Bayes. This post is not about the theorem itself, its meaning or its demonstration. If you are interested to know more, the YouTube channel 3Blue1Brown provides excellent videos on the topic:

The quick proof of Bayes’ theorem

Bayes theorem

For our purpose, you just have to accept the following statement:

Your chances to be actually infected if you tested positive are equal to the chances to be infected in the first place multiplied by the chances of testing positive if actually infected, scaled to the size of the population that tested positive (whether actually infected or not).

In mathematical terms, we would write:
(P(X) means “Probability of X”, the vertical bar “|” represents a conditional probability, the probability that what is on the left side is true given that what is on the right side is true)

P(Infected | Positive) = P(Infected) x P(Positive | Infected) / P(Positive)

This equation, Bayes’ theorem, comes from the fact that:
P(Positive) x P(Infected | Positive) = P(Infected) x P(Positive | Infected)
This is obvious from the image below. Whether you draw the left circle first, then the second, or the other way around, the overlapping surface is still the same.

The denominator, P(Positive), representing all people who tested positive, is the sum of the people who rightly tested positive while being infected and the people who wrongly tested positive while not being infected:

P(Positive) = P(Infected) x P(Positive | Infected) + P(NotInfected) x P(Positive | NotInfected)

This probability, P(Infected | Positive), is particularly important in the cases of antibody tests. We do not want to tell a person they are immune if they are not!

Similarly, we can compute the chances that someone who tested negative is actually not infected. That is very important at the beginning of the epidemics when we want to stop infected people to spread the disease.

P(NotInfected | Negative) = P(NotInfected) x P(Negative | NotInfected) / P(Negative)

The denominator, P(Negative), representing all people who tested negative, is the sum of the people who rightly tested negative while not being infected and the people who wrongly tested negative while in fact being infected:

P(Negative) = P(NotInfected) x P(Negative | NotInfected) + P(Infected) x P(Negative | Infected)

Let’s see what we get with actual values. We have three parameters and their complement. Let’s say we have a disease affecting 5% of the population (the prevalence).
P(Infected) = 0.05
P(NotInfected) = 0.95

80% of infected people are caught by the test (its sensitivity).
P(Positive | Infected) = 0.8
P(Negative | Infected) = 0.2

95% of the people who are not infected will not be tested positive (the specificity).
P(Negative | NotInfected) = 0.95
P(Positive | NotInfected) = 0.05.

Now, if you are tested positive, what are the chances you are actually immune?

0.05 x 0.8 / (0.05 x 0.8 + 0.95 x 0.05) = 0.457

46%! In other words, there are 54% chances that you are not actually immune despite being labeled as such by the test… Conversely, if you are tested negative, the chances that you are actually infected are 0.2%. The number looks pretty small, but this can be sufficient to “leak” an infectious patient outside. And this number grows as the prevalence does. How much? The plot below depicts the evolution of probabilities to be correctly tested positive and negative when the proportion of the infected population increases.

That looks pretty grim, doesn’t it? One way of improving the results is obviously to have better tests. However, the “return on investments” becomes increasingly limited as the quality of tests improves. Another solution, lies in multiple testing, if possible with different tests. This is, for instance, the basis of combined test for Down’s Syndrome. I will let you work out the math if you get twice the same result with two independent tests.

Note about Covid-19’s lethality

Why did I write above that the accuracy of testing was relevant for estimating the lethality of the disease (the Infection Fatality Rate, IFR)? Below is a plot of the ratio number of deaths per number of cases towards the number of tests per million people, for all countries that reported at least 1 death and at least 10 tests (data from 10 April 2020).

It is pretty clear that there is a correlation, the more tests being done, the lower the estimated fatality. This shows that we probably overestimate the lethality of the disease, and underestimate its prevalence (and therefore its infectiosity). Whether this result is accurate or not, the ability to correctly infer the actual number of people infected and/or immune is pretty crucial. Moreover, the sensitivity and specificity of the tests used by different countries should be taken into account when estimating prevalence and fatality rate.