By Nicolas Gambardella
A crucial part of any computational modelling is getting parameter values right. By computational model, I mean a mathematical description of a set of processes that we can then numerically simulate to reproduce or predict a system’s behaviour. There are many other kinds of computational or mathematical models used in computational biology, such as 3D models of macromolecules, statistical models, machine learning models and more. While some concepts dealt with in this blog post would actually be relevant, I want to limit the scope of this post to what is sometimes called “systems biology” models.
So, we have a model that describes chemical reactions (for instance). The model behaviour will dictate the values of some variables, e.g. substrate or product concentrations. We call those variables “dependent” (“independent variables” are variables whose values are decided before any numerical simulation or whose values do not depend on the mathematical model, such as “time” for standard chemical kinetics model). Another essential set of values that we have to fix before a simulation consists of the initial conditions, such as initial concentrations.
The quickest way to get cracking is to gather the variable values from previous models (found for instance in BioModels), from databases of biochemical parameters such as Brenda or SABIO-RK, or from patiently sieving scientific literature. But what if we want to improve the values of the variables? This blog post will explore a few possible ways forward using the modelling software tool COPASI, namely, sensitivity analysis, picking up variable values and looking at the results, parameter scans, optimisation, and parameter estimation.
Loading a model in COPASI
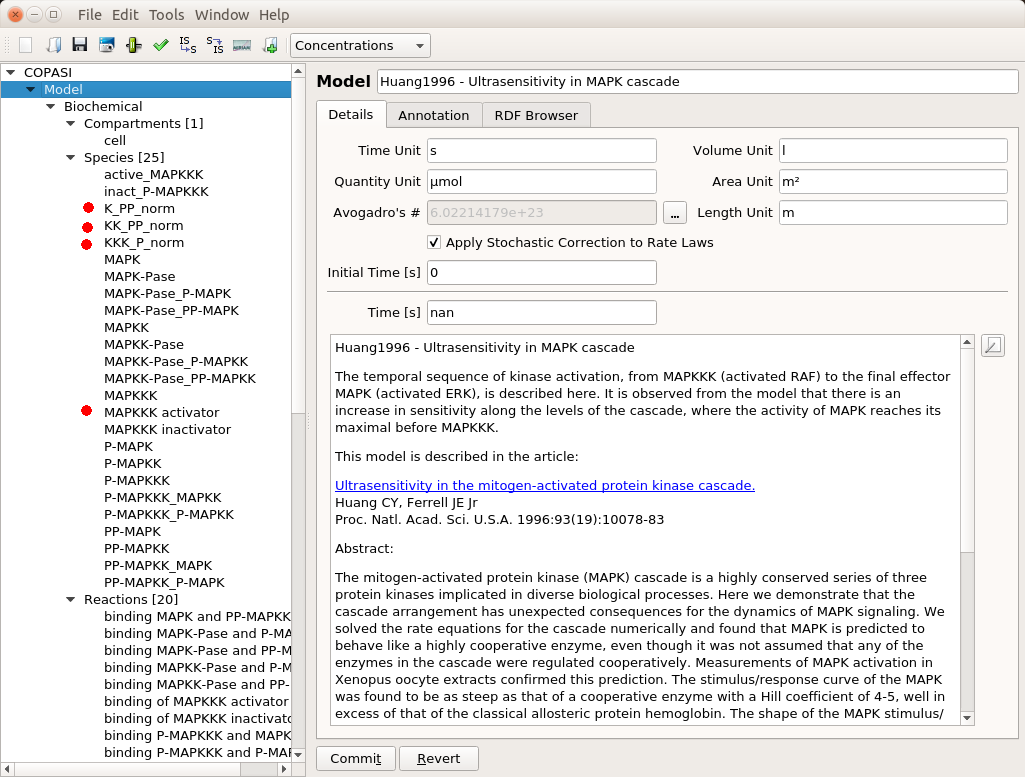
First, we need to have a model to play with. The post will use the model of MAPK signalling published by Huang and Ferrell in 1996. You can find it in BioModels where can download the SBML version and import it in COPASI. Throughout this post, I will assume the reader masters the basic usage of COPASI (create reactions, run simple simulations, etc.). You will find some introductory videos about this user-friendly, versatile, and powerful tool on their website.
The model presents the three-level cascade activating MAP kinase. MAPK, MAPKK, and MAPKKK mean Mitogen-activated protein kinase, Mitogen-activated protein kinase kinase, and Mitogen-activated protein kinase kinase kinase, respectively. Each curved arrow below represents three elementary reactions: binding and unbinding of the protein to an enzyme, and catalysis (addition or removal of a phosphate).
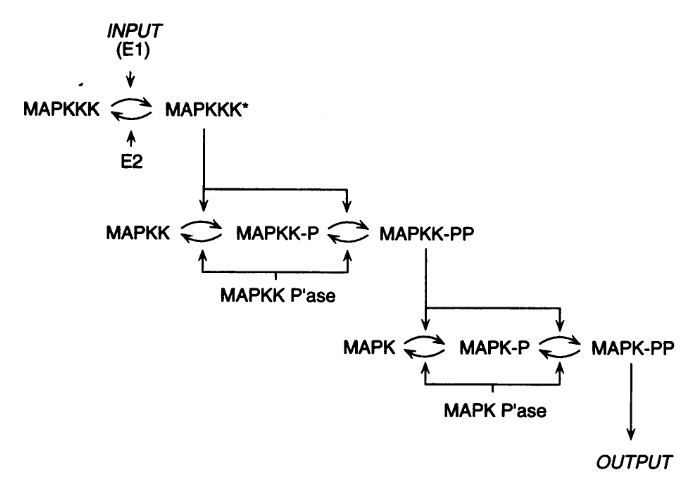
The top input E1 (above) is called MAPKKK activator in the model. To visualise the results, we will follow the normalised values for the active (phosphorylated) forms of the enzymes K_PP_norm, KK_PP_norm and K_P_norm, that are just the sums of all the molecular species containing the active forms divided by the sums of all the molecular species containing the enzymes (NB: Throughout the screenshots, the red dots are added by myself and not part of COPASI’s GUI).
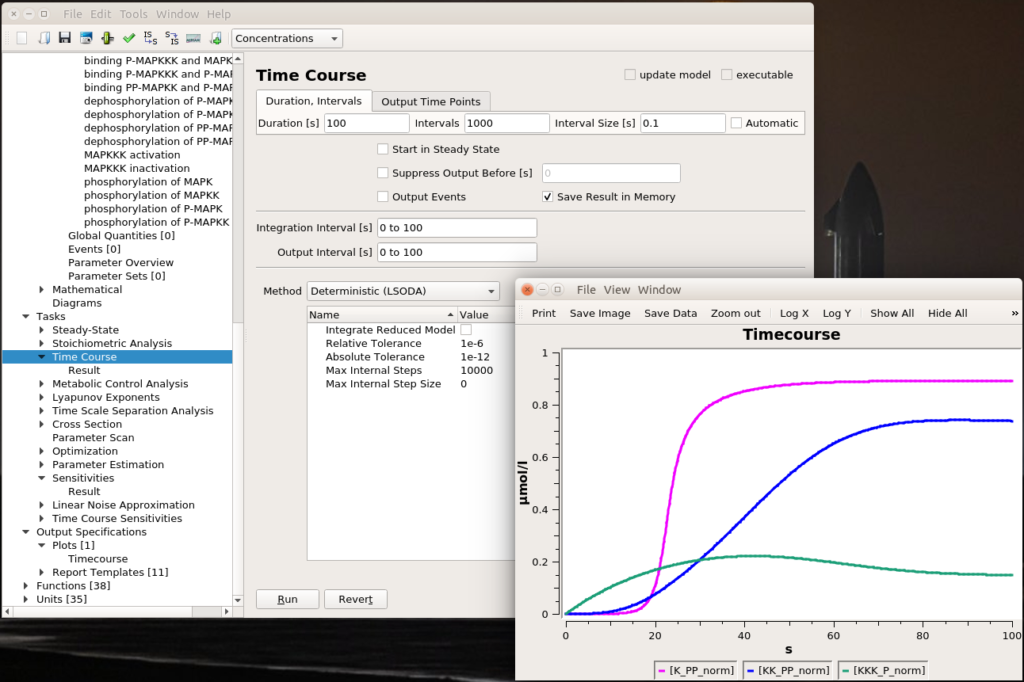
Let’s run a numerical simulation of the model. Below you see the activation of the three enzymes, with the swift and supra-linear activation of the bottom one, MAPK, one of the hallmarks of the cascade (the others being an amplification of the signal and an ultrasensitive dose-response which allows to fully activate MAPK with only a touch of MAPKKK activation).
Sensitivity analysis
The first question we can ask ourselves is “What are the parameters that values affect the most the output of our system?”. To do so, we can run a sensitivity analysis. COPASI will vary a bit all the parameters and measure the consequences of these changes on the results of a selected task, here the steady-state of the non-constant concentrations of species.
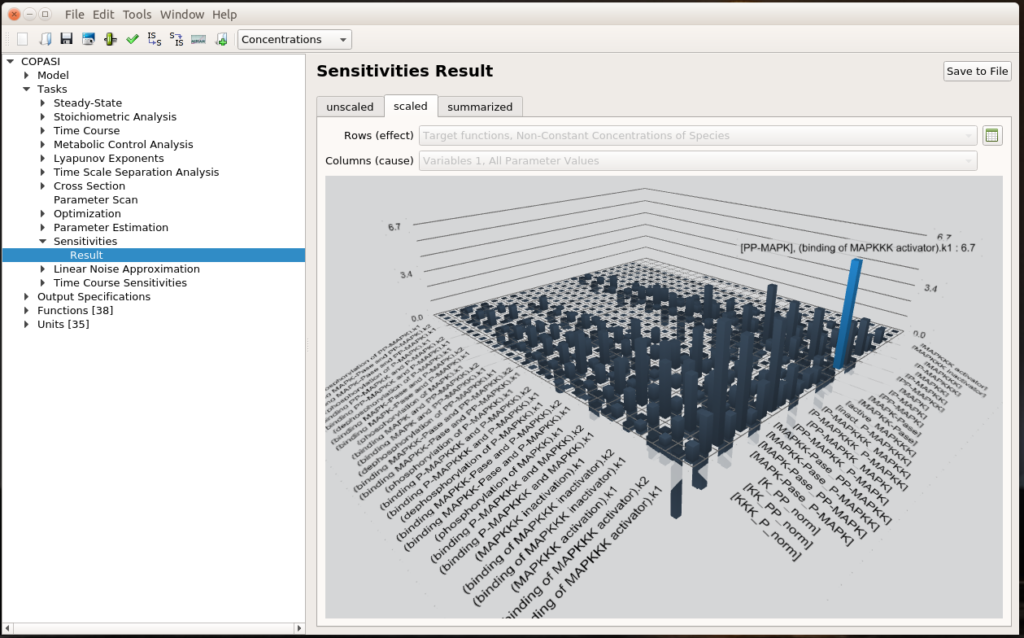
We see that the most important effect is the impact of MAPKKK activator binding constant (k1) on the concentration of PP-MAPK, which happens to be the final output of the signalling cascade. This is quite relevant since the MAPKKK activator binding constant basically transmits the initial signal at the top of the cascade. You can click the small spreadsheet icon on the right to access coloured matrices of numerical results.
Testing values
All right, now we know which parameter we want to fiddle with. The first thing we can do is visually look at the effect of modifying the value. We can do that interactively with a “slider“. Once in the timecourse panel, click on the slider icon in the toolbar. You can then create as many sliders as you want to set values manually. Here, I created a slider that can vary logarithmically (advised for most model parameters) between 1 and 1 million. The initial value, used to create the timecourse above, was 1000. We see that sliding to 100 changes the model’s behaviour quite dramatically, with very low enzyme activations. Moving it well above 1000 will show that we increase the speed of activation of the three enzymes, increase the activation of the top enzyme, albeit without significant gain on K-PP, our interesting output.
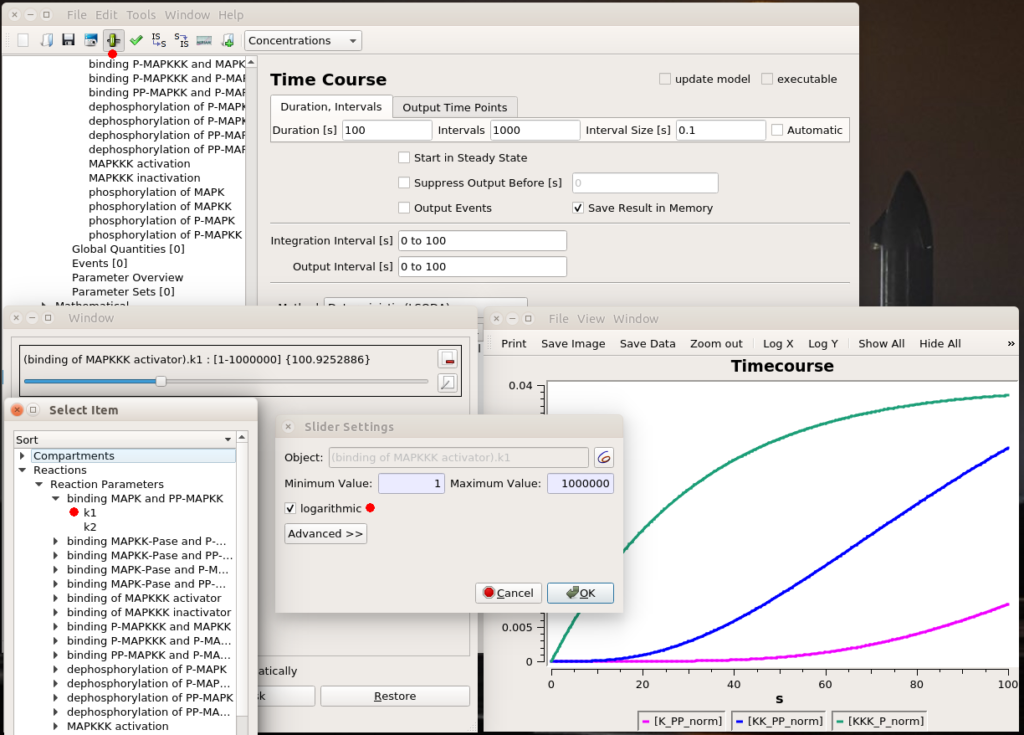
Parameter scans
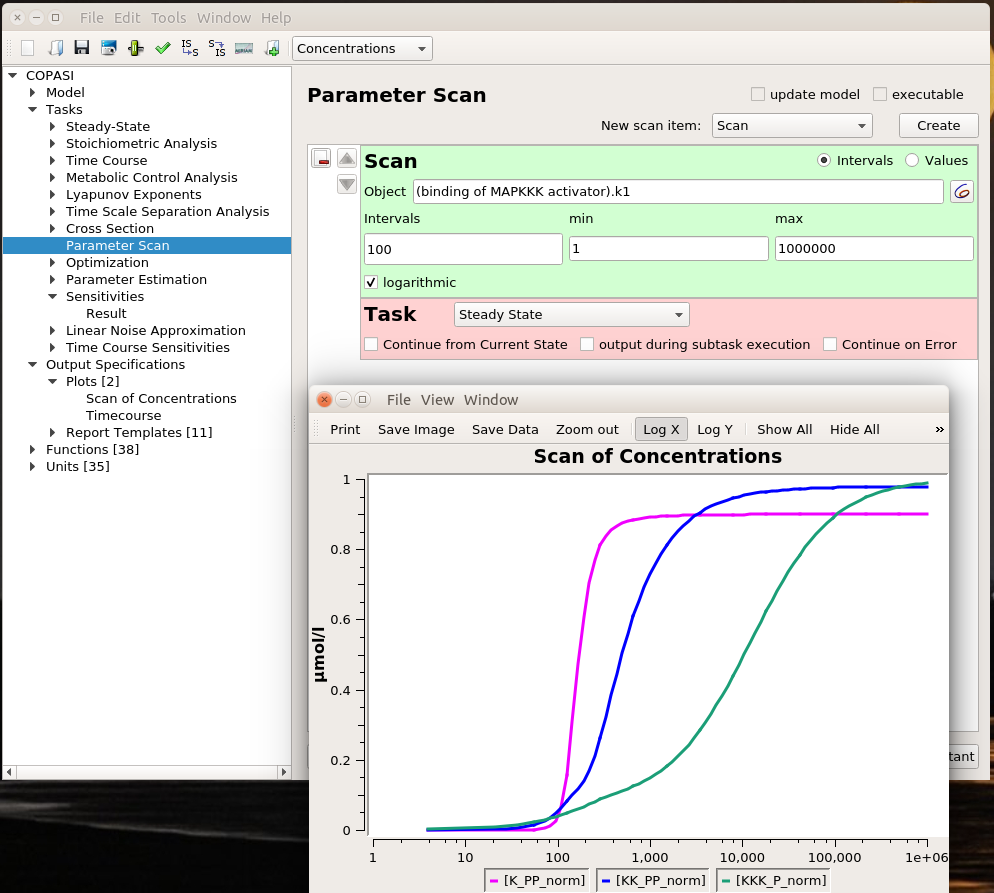
Playing with sliders is great fun. But this is not very precise. And if we want to evaluate the effect of changing several parameters simultaneously, this can be extremely tedious. However, we can do that automatically thanks to COPASI’s parameter scans. We can actually repeat the simulation with the same value (useful to repeat stochastic simulations), systematically scan parameter values within a range, or sampling them from statistical distributions (and nest all of these). Below, I run a scan over the range defined above and observe the same effect. To visualise the scan’s results, I created a graph that plotted the active enzyme’s steady-state versus the activator binding constant.
Optimisation
All that is good, but I still have to look at curves or numerical results to find out the best value for my parameter. Ideally, I would like COPASI to hand me directly the value. This is the role of optimisation. Optimisation if made up of two parts: the result I want to optimise and the parameter to change to optimise it. I will not discuss the possibility to optimise a value. There are many cases for which optimisation is just not possible. For instance, it is not possible to optimise the production of phosphorylated MAPK. Whatever upper bound we would fix for the activator binding constant, the optimal value would end up on this boundary. In this example, I decided to maximise the steady-state concentration of K_PP for a given concentration of KKK_P, i.e. getting the most bang for my buck. As before, the parameter I want to explore is the MAPKKK activator binding constant. I fix the same lower and upper bound as before. COPASI offers many algorithms to explore parameter values. Here, I chose Evolutionary Programming, which offers a good balance between accuracy and speed.
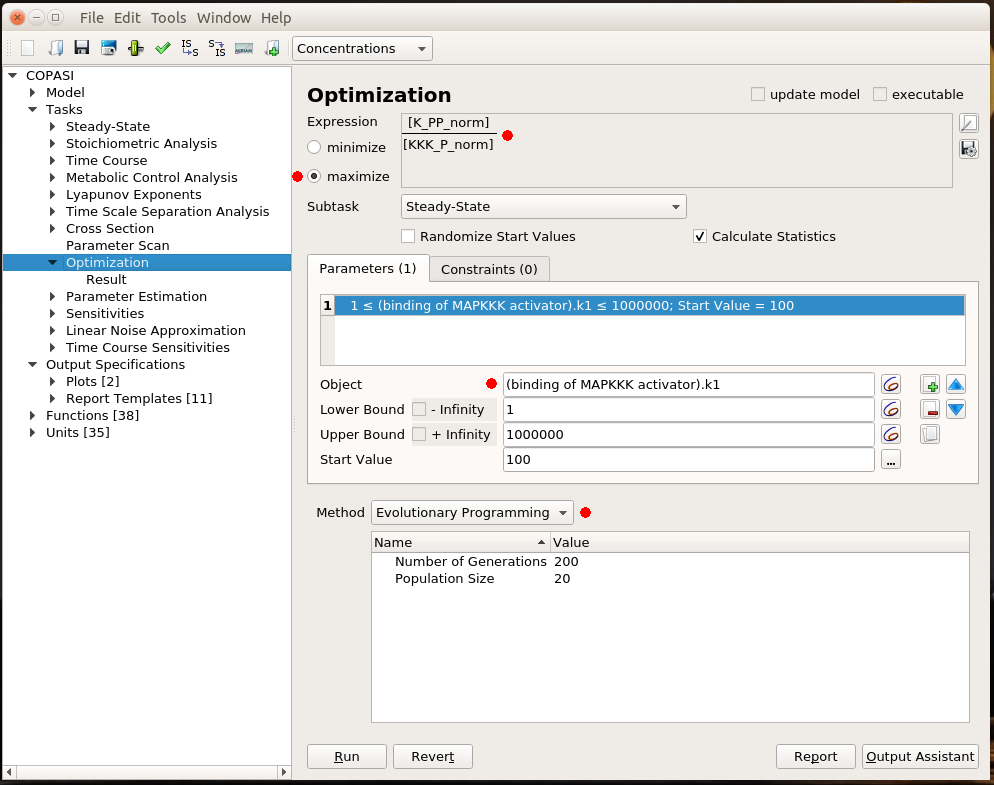
The optimal result is 231. Indeed, if we look at the parameter scan plot, we can see that with a binding constant of 231, we get an almost maximal activation of MAPK with minimal activation of MAPKKK. Why is this important? All those enzymes are highly connected and will act on downstream targets right, left, and centre. In order to minimise side effects, I want to activate (or inhibit) protein as little as necessary. Being efficient at low doses also helps with suboptimal bioavailability. And of course, using 100 times less of the stuff to get the same effect is certainly cheaper, particularly for biologics such as antibodies.
Parameter estimation
We are now reaching the holy grail of parameter search, which is parameter estimation from observed results. As with optimisation, this is not always possible. It is known as the identifiability problem. Using the initial model, I created a fake noisy set of measurements, which would, for instance, represent the results of Western blot or ELISA using antibodies against phosphorylated and total forms of RAF, MEF, and ERK, which are specific MAPKKK, MAPKK, and MAPK.
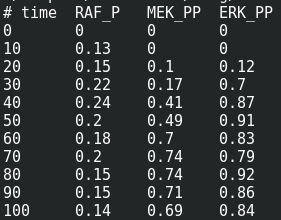
I can load this file (immuno.txt on the screenshot) in COPASI, and map the experimental values (automatically recognised by COPASI) to variables of the model. Note that we can load several files, and each file can contain several experiments.
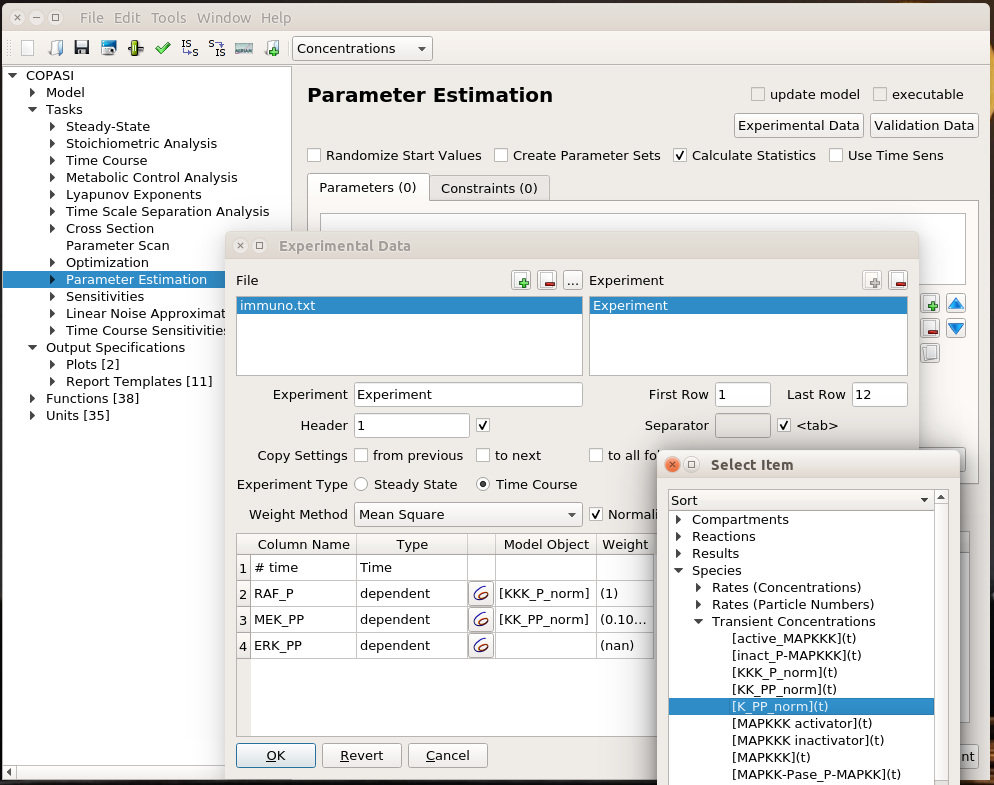
I can then list the parameters I want to explore, here the usual activator binding constant, between 1 and 1 million. Note that we can use only some of the experiments in the estimation of given parameters. This allows building extremely powerful and flexible parameter estimations.
We can use the same algorithms used in optimisation to explore the parameter space. The plot represents the best solution. Dashed lines link experimental values, continuous lines represent the fitting values, and circles are the error values.
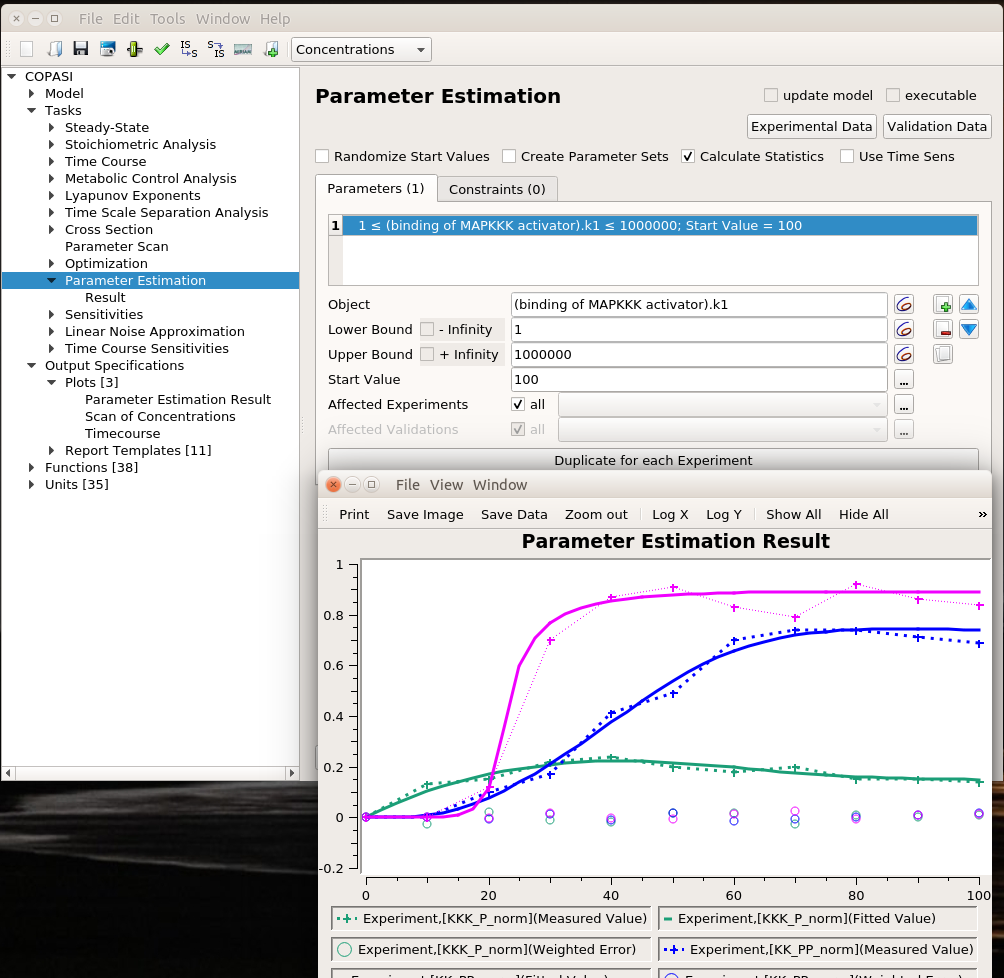
The value estimated by COPASI for the binding constant is 1009. The “experiment” was created with a value of 1000. Not bad.
This concludes our overview of parameter exploration with COPASI. Note that this only brushes up the topic and I hope I picked your curiosity enough for you to read more about it.
Do you have a model that you want to improve? Do you need to model a biological system but do not know the best method or software tool to use? Drop me a message and I will be happy to have a chat.